Am Samstag steht ein Event an was, denke ich, für die meisten jetzt nicht allzu interessant klingt: NCPC: 5-Stunden Comptetitive-Coding-Contest. War echt witzig und Magnus, Ragul und ich haben uns auch echt gut geschlagen. Der Contest ist zeitgleich an allen nordischen Unis und die Veranstalter stellen Snacks und Getränke zur Verfügung. Für jedes gelöste Problem gibt einen Luftballon in einer anderen Farbe, so kann man beobachten, wie sich, die anderen so schlagen. Außerdem kann man immer zähneknirschen, wenn ein anderes Team einen Ballon erhält, den man selbst noch nicht hat. Die Mischung aus Mathematik, Logik und dem Programmieren von effizienten Algorithmen taugt mir. Danach gabs noch eine Siegerehrung, einen Livestream mit Besprechung der Probleme und die beste Pizza die ich bisher in Finnland hatte.
Für alle interessierten: Ein echt feines Beispiel vom Contest:
–> Factor-Full Tree

> 5
> 1 2
> 1 3
> 3 4
> 3 5
< 1 2 3 21 33
So dann mal los. PS. Wir waren verdammt knapp dran dies Problem im Contest zu lösen, haben aber eine Kleinigkeit übersehen und immer „Falsche Antwort“ als Fehler erhalten.
Also warum geht es eigentlich in diesem Beispiel? Es geht darum, eine Reihe an Zahlen zu generieren, die zu einem eindeutigen Baum (Tree) rekonstruiert werden können. Dabei wird immer mit der kleinsten Node als Root/Main-Node begonnen. Dann wird der Baum deterministisch aufgebaut, indem immer alle Nodes als „Children“ der zuvorkommenden Node hinzugefügt werden, wenn sie nur von den jeweiligen Parent-Nodes ohne Rest geteilt werden können.
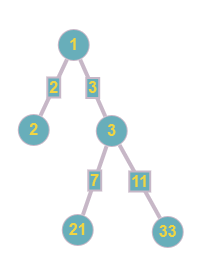
Der Graph des Beispieles ergibt sich also so: zB. 33 kann durch 1 und 3 ohne Rest geteilt werden, also sind die beiden Nodes Prarents von 33 während dasselbe mit den Nodes 2 und 21 nicht möglich ist. Wählt man die Zahlen geschickt, so ist das Erstellen des Graph-Trees deterministisch/eindeutig möglich und der Graph aus der Angabe kann rekonstruiert werden. (ps don’t judge me aber i hab keinen Plan wie man Graph wirklich schreibt)
Wer sich ein paar Gedanken über Faktorisierung von Zahlen macht, kommt schnell drauf: Wenn die Multiplikationsfaktoren (auf den Ästen) immer unterschiedliche Primzahlen sind, bekommt man einen eindeutigen Baum. Die Angabe sagt auch: Es gibt maximal 60 Nodes. Also schnell 60 Primzahlen suchen und den Baum konstruieren. Sollte in einer Sekunde Rechenzeit leicht machbar sein. Haben wir auch so umgesetzt. Abgegeben – und „Falsche Antwort“. Und jetzt wirds wahrscheinlich für nicht Informatiker schwierig. Aber die Angabe sagt, dass alle Nodes kleiner 10^18 sein müssen. Daher haben wir garnicht lange über Datentypen nachgedacht, weil sich das Ganze mit uint64 ausgehen muss. Bei falschen Antworten ist es oft eine gute Idee ein einfaches Script zu schreiben das eigene Testcases generiert. Ein einfacher Testcase: Alle Nodes hängen in einer Reihe ohne je zu verzweigen. Und wir sehen uns das Ergebnis unseres Programms an. Ab ca den 15 Wert springen die Zahlen wild umher. Schnell kommen wir darauf: Das Ganze ist ein massiver Overflow. Kurze Überlegung ergibt: Wir sind dumm. Nehmen wir an, der Durchschnitt der ersten 60 Primzahlen ist 10 (grobe Unterschätzung). Dann kommt man bei dem Baum für die letzte Node auf einen Wert von 10^59. Ist nur ein kleines bisschen größer als 10^18. Wenigstens kennen wir jetzt das Problem.
Nach einiger Überlegung kommen wir drauf, dass man den Multiplikationsfaktor von der Parent Node für eine Child-Node wiederverwenden kann. Und siehe da: 2^59 = 5.76*10^17. Nice. Also: Vor dem Definieren der Faktoren ein Tree-Traversal und den Leaf-Nodes werden vom tiefsten bis zu dem flachsten Baum die Primzahlen in aufsteigender Reihenfolge zugewiesen, wobei immer die geringste Zahl der Parent Nodes weiterverwendet wird. Unsere eigenen Testcases funktionieren. Erneut abgeben und: „Falsche Antwort“. Auf diesem Stand bleibt die Aufgabe leider bis zum Ende des Wettbewerbs.
Danach in der Auflösung sehen wir das Problem. Unsere Definition von tiefster Baum. Stellen wir uns vor, es gibt einen Baum, der sich bei der Basis-Node einmal verzweigt und dann in zwei parallelen Reihen je 25 Nodes lang verläuft. An einem der beiden Stränge hängen an der 25. Node noch parallel alle restlichen 9 Nodes. Diese 9 Nodes haben unseren Algorithmus zufolge eine größere Tiefe als der einzlene 25 Nodes lange Strang. Daher bekommen die 9 Nodes die neun kleinsten Primzahlen. Die zehntkleinste Primzahl ist 29. Kurze Überschlagsrechnung für den anderen Strang: 29^24 ist wieder geringfügig größer als 10^18. Verdammt. So ein misst.
Lösung: Man hätte den Algorithmus so abändern müssen, dass, wenn einem Strang schon eine Primzahl zugewiesen wurde die Werte der Nodes vorberechnet werden. Anschließend wird die Tiefe einer Leaf-Node folgendermaßen berechnet: m sei die kleinste noch nicht genutzte Primzahl, xNode sei die nächste Node im Tree die schon einen Wert bekommen hat: Tiefe = m-Logarithmus des Wertes der xNode + Tiefe der Leaf-Node bis zur xNode. Das würde garantieren, dass der Tree ideal/kleinstmöglich aufgebaut wird. Im obigen Beispiel wird dem 25-Strang die 3 zugewiesen und das Erstellen aller Bäume unter den Bedingungen der Angabe ist möglich. Wäre mit einer Stunde mehr sicher lösbar gewesen. Aber allein die Länge dieses Betrags ist ein Testament dafür, wie gern ich mich mit solchen Dingen beschäftige. ps. Gratuliere an alle, die der Beschreibung bis jetzt gefolgt sind xD.

Am Sonntag geht es früh los, denn wir wollen nach Tampere. Ist eine recht schöne Stadt mit zig Kirchen, Parks und Backsteingebäuden . Am Morgen geht jedoch ein richtig zahniger Wind der uns ohne weiteres zu Museumsbesuchen überredet. Die Musen sind interaktiv und abwechslungsreich gestaltet – was uns recht gut gefällt. Wir sehen uns die textilindustrielle Geschichte, Posti, finnische Computerspielgeschichte (mit vielen Stationen zum Ausprobieren: mit Mario, Pac-Man, Donkey-Kong, Ping-Pong und vielem mehr), eine Hockeyausstellung mit Schusssimulator und schlussendlich auch die Ausstellung „Fantastinen Floppi“ an. Und diese ist in Anbetracht der Geschichte von Tampere sehr interessant: Hier wurde die wohl bekannteste Firma Finnlands gegründet, die in den letzten 15 Jahren von Weltmarktführer zu nicht mehr relevant gefloppt ist. Wer es bis jetzt nicht erraten hat: Nokia.

Dabei waren die Smartphones zu der Zeit schon genial. Meiner Meinung nach wurde mit der Fold & Swivel-Technologie der Höhepunkt der Smartphone-Formfaktoren erreicht. Ich meine, das Handy ist handlich und 17x robuster wie jedes dieser zarten Gorilla-Glass & Space-Grade-Alluminum Smartphones. Zudem hatte das Handy eine heute unglaubliche „all-week battery life“ und eine Zeiss-Optik mit 3-fachem optischen Zoom. Und dieses Paket 2007. Tja leider hats ohne Touch dann halt doch nicht geklappt und jetzt gibt es eine Flopp-Ausstellung.
Zum Sonnenuntergang sind wir dann noch zum Pyynikin-Watchtower spaziert, und haben bei besserem Wetter einen bewundernswerten Sonnenuntergang genossen. Als großer Ausblick-Fan hat mich auch die Sicht auf die zwischen Seen liegende Stadt begeistert. Also der Turm ist meinem Meinung nach die Top-Attraktion in der Stadt.
Tja – am Donnerstag sind wir wieder was Sportliches angegangen. Oder zumindest war das der ursprüngliche Plan. Die Orienteering Association bietet alle zwei Wochen ein Training an, bei dem eine Karte und Checkpoints vorbereitet werden die dann abgeklappert werden müsse. Wir werden wie Experten mit Kompass, Stirnlampe und Karte ausgestattet und schon wird losgerannt. Hat am Anfang auch recht gut geklappt, da wir uns ganz gut an den anderen Teilnehmern „orienteeren“ konnten. Problematisch wurde es bereits bei Checkpoint 5. Keine Menschenansammlung an einem Punkt. Und jetzt gehts daran: Finde in einem Wald mit einer Karte einen blauen & roten Streifen. Stellt sich heraus: Das ist wesentlich schwerer als von Punkt zu Punkt zu laufen und es geht weit mehr Zeit für das Suchen drauf. Holly smokes – das fühlt sich in so vielen Fällen unmöglich an. Mit Höhenlinien, Steinen, Wegen (wir haben vier Level von Wegen definiert: Primary, secondary and secondary-secondary should’t exist) soll man einen Punkt auf 10 Meter genau finden. Tut man das nicht ist die Suche nach dem Faden recht aussichtslos. Wirklich problematisch wurde es dann bei Checkpoint 10: Wir wollten nicht den direkten Weg nehmen, weil die Gegend unter Wasser gestanden ist, und dieser Umweg hat uns ein bisschen desorientiert. Wir haben den Checkpoint für Ewigkeiten gesucht und das Gelände einer Doktorarbeit würdig untersucht. Alle 5 Minuten haben wir beschlossen, diese Stelle ist jetzt sicher der richtige Ort. Doch statt Fäden finden wir nur Hasen. Irgendwann disqualifizieren wir uns selbst und überspringen den Checkpoint. Bei Checkpoint 25 schreiben uns die Organisatoren, sie werden nicht mehr im Ziel warten und wir sollen uns melden, wenn wir bei der Sauna sind, damit sie uns die Türe öffnen. Hat uns aber auch nicht unterkriegen können, denn glücklicherweise haben wir (Miquel und ich) uns von Anfang an entschieden den Lauf gemeinsam zu machen und die Motivation war stets hoch. Am Ende haben wir es dann doch noch zum letzten Checkpoint geschafft: Ideale Strecke: ca 7 km. Unsere Zeit: 2h 37min und dann noch disqualifiziert (obwohl wir sicher da waren und nur den Streifen nicht gefunden haben xD ). Die Sauna danach kam uns dann doch sehr gelegen. Alles in allem eine coole Erfahrung und wenn es sich zeitlich ausgeht, werden wir es sicher nochmals probieren.








